My Blog | 详情

1.tree 树定义：

又叫：字典树，前缀树，单词查找树，键树。

是一种有序的多叉树。用于保存关联数组，

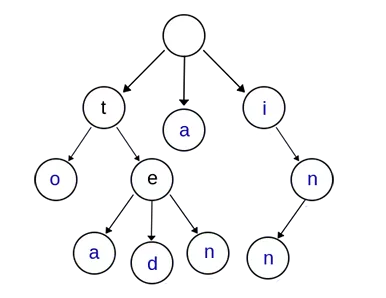
2.tree 树性质：

根节点规定为空字符串，非根节点至少包含一个字符
从根节点到某一个节点，路径上经过的字符连接起来，组成的字符串为这个节点所对应的字符串
每个节点的所有子节点包含的字符互不相同

通常在构造 tree 树时，会在节点上设置一个标志，表明该节点代表的字符串是否构成单词（或 ”关键字“）。

3.tree 树优缺点：

字典树这种数据结构的设计思想很简单，就是用空间换时间，提高字符串查找效率。

优点：

插入合查询效率都是 O(n)，n 为字符串长度
对比 hash，虽然理想状态hash 的查找效率是 O(1) ，但这取决于 hash 函数好坏，如果冲突多，则效率不一定比字典树高
不同的关键字在树中一定不会冲突
字典树只有在允许一个节点关联多个值的情况下，才有类似hash 碰撞的情况产生
trie 树不用求 hash 值，对短字符串效果极佳。
可以进行字符串排序（按字典序）

缺点：

空间成本较高
当 hash 函数较好时，查询效率 hash 表更高

4.应用：

1、字符串检索

检索/查询功能是Trie树最原始的功能。思路就是从根节点开始一个一个字符进行比较：

如果沿路比较，发现不同的字符，则表示该字符串在集合中不存在。
如果所有的字符全部比较完并且全部相同，还需判断最后一个节点的标志位（标记该节点是否代表一个关键字）。

struct trie_node
{
   bool isKey;   // 标记该节点是否代表一个关键字
   trie_node *children[26]; // 各个子节点
};

2、词频统计

Trie树常被搜索引擎系统用于文本词频统计。

struct trie_node
{
   int count;   // 记录该节点代表的单词的个数
   trie_node *children[26]; // 各个子节点
};

思路：为了实现词频统计，我们修改了节点结构，用一个整型变量count来计数。对每一个关键字执行插入操作，若已存在，计数加1，若不存在，插入后count置1。

注意：第一、第二种应用也都可以用 hash table 来做。

3、字符串排序

Trie树可以对大量字符串按字典序进行排序，思路也很简单：遍历一次所有关键字，将它们全部插入trie树，树的每个结点的所有儿子很显然地按照字母表排序，然后先序遍历输出Trie树中所有关键字即可。

4、前缀匹配

例如：找出一个字符串集合中所有以ab开头的字符串。我们只需要用所有字符串构造一个trie树，然后输出以a->b->开头的路径上的关键字即可。

trie树前缀匹配常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。

5、作为其他数据结构和算法的辅助结构

如后缀树，AC自动机等。

5. demo：

//
// Created by admin on 2021/3/30.
//

#include<iostream>
#include<string>

using namespace std;

#define ALPHABET_SIZE 26

typedef struct trie_node
{
    int count;  // 记录该节点代表单词的个数
    trie_node *children[ALPHABET_SIZE]; // 各个子节点
}*trie;

trie_node* create_trie_node()
{
    trie_node* pNode = new trie_node();
    pNode->count = 0;
    for(int i = 0; i < ALPHABET_SIZE; i++) {
        pNode->children[i] = NULL;
    }
    return pNode;
}

void trie_insert(trie root, char* key)
{
    trie_node* node = root;
    char* p = key;
    while(*p) {
        if (node->children[*p - 'a'] == NULL) {
            node->children[*p - 'a'] = create_trie_node();
        }
        node = node->children[*p - 'a'];
        p++;
    }
    node->count += 1;
}

// 查询：不存在返回0，存在返回出现的次数
int trie_search(trie root, char* key)
{
    trie_node* node = root;
    char* p = key;
    while(*p && node != NULL) {
        node = node->children[*p - 'a'];
        p++;
    }
    if (node == NULL) {
        return 0;
    } else {
        return node->count;
    }
}

int main() {
    char keys[][8] = {"the", "a", "there", "answer", "any", "by", "bye", "their"};
    trie root = create_trie_node();

    for(int i = 0; i < 8; i++) {
        trie_insert(root, keys[i]);
    }

    char s[][32] = {"Present in trie", "Not present in trie"};
    printf("%s occurrence times: %d\n", "the", trie_search(root, "the"));
    printf("%s occurrence times: %d\n", "these", trie_search(root, "these"));
    printf("%s occurrence times: %d\n", "their", trie_search(root, "the"));
    printf("%s occurrence times: %d\n", "thaw", trie_search(root, "thaw"));

    return 0;
}